Vegas lines and odds are normally great tools in DFS to derive projected outcomes. Given a spread and an over/under total, you can reverse-engineer a pretty good estimate of the most likely outcome for a game. Throw in some supplemental metrics (player prop bets lines, usage rate, receiver targets, etc.), and you can even get a good idea of what individual players will do. So it’s natural that a lot of people use PGA Vegas odds as a part of their DFS analysis. To be clear, Vegas odds to win are a pretty good estimate for what’s going to happen in a golf tournament. If you don’t want to derive those outcomes yourself, the Vegas odds provide a quick-and-dirty number you can use that saves you a lot of work. However, there are two golf-specific complications that undercut the value of Vegas odds in PGA:
- Vegas odds are not independent of players’ prices on DraftKings. In fact, they are strongly correlated. This severely undercuts their usefulness in finding value, since that requires projecting a player’s outcome independent of their pricing.
- Vegas odds to win are biased toward players with high upside and are not indicative of average outcome. That makes Vegas odds a poor choice in finding high-value, low-upside players, who are staples of cash games.
The first point deserves some further exploration down the road in a more-detailed discussion of correlated variables and how value is fundamentally different in PGA pricing. It’s the second point I want to explore right now, because it has more practical takeaways for roster construction.
Vegas Odds and Upside Bias
Let’s take a look at some of the lines offered from the 2016 Masters, from both odds to win and head-to-head matchups (which I think are far more valuable than odds to win, but that’s another article). I want to focus on one pair of players in particular, Adam Scott and Rickie Fowler.
Here’s one table:
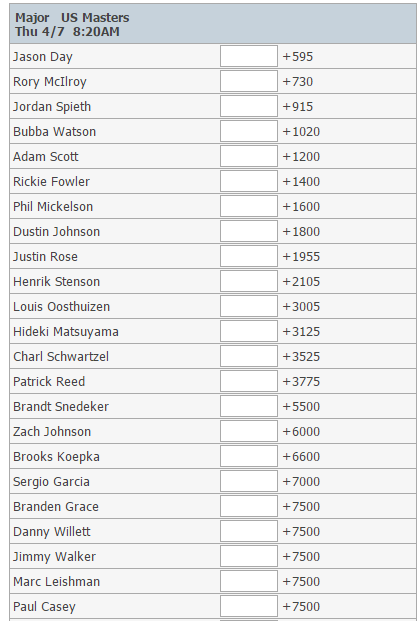
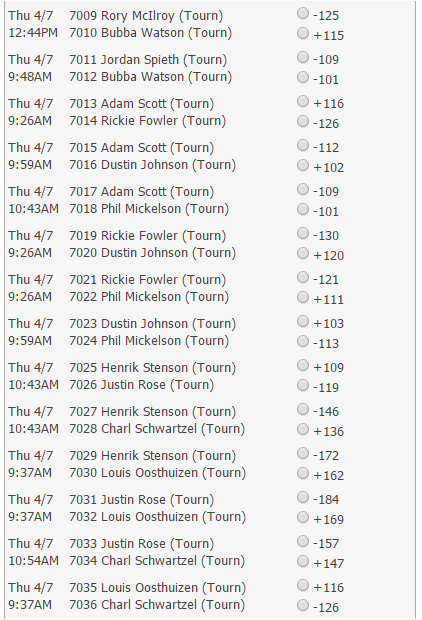
- Rickie Fowler is expected to do better than Adam Scott.
- Rickie Fowler has a worse chance of winning the tournament than Adam Scott.
Wrap your mind around that for a bit. Those statements seem to be directly at odds with one another. However, here’s an illustration of how those two statements can live in harmony. Let’s take an exaggerated estimate of what the distributions of their golf scores might be under these two statements:

Fowler can be expected to do better on average, since the center of his distribution is to the right of Scott’s. However, Scott has a much wider range of outcomes, so the probability that he has a very good score is much higher than Fowler’s. This is how both of those statements are compatible with each other.
So if we know that DraftKings prices correlate very strongly with odds to win, and odds to win is measured by some combination of average score and upside, then we know that upside is a strong component of a player’s price. However, for cash games, we want something very different: minimal upside, high average score. It stands to reason that there are such players whom Vegas-based pricing is systematically undervaluing, since pricing has an upside component. How do we find them? We’ll go over some helpful metrics in next week’s article.





